10月20日,東南大學丘成桐中心研究員Ryo Suzuki與合作者在物理學著名期刊《Physical Review Letters》上發表題為Tensionless Limit of Pure–Ramond-Ramond Strings and AdS3/CFT2 的學術論文。這一工作為AdS3/CFT2對偶研究帶來曙光。AdS/CFT對偶在全息理論的研究中占據著核心地位。根據AdS/CFT對偶,AdS3時空中的弦理論與某種二維共形場論 (CFT2) 是等價的。CFT是一種高度對稱的量子場論,可用于描述包括黑洞和超導體在內的很多物理系統。
具體來說,這篇論文分析了與D1和D5膜系統密切相關的Ramond-Ramond AdS3×S3×T4時空中的弦理論。而在AdS3/CFT2對偶的研究中,這種弦理論的具體CFT對偶長期以來都無法確定。Suzuki所在的研究小組利用一種新數學技術——鏡像TBA方程——來研究 AdS3×S3×T4時空弦理論的能譜,解決了這一難題。TBA方程是一組可以用來描述量子可積系統能級的非線性積分方程。他們發現,在弦張力較小的情況下對反常維數(anomalous dimension)的領頭階貢獻來自于世界面(world sheet)的無能隙激發,這為表征其對偶CFT2提供了重要線索。
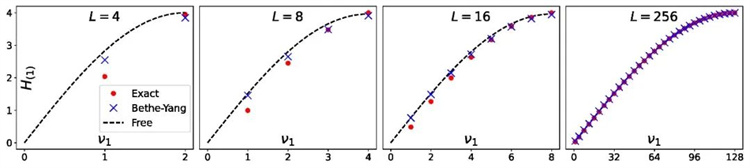
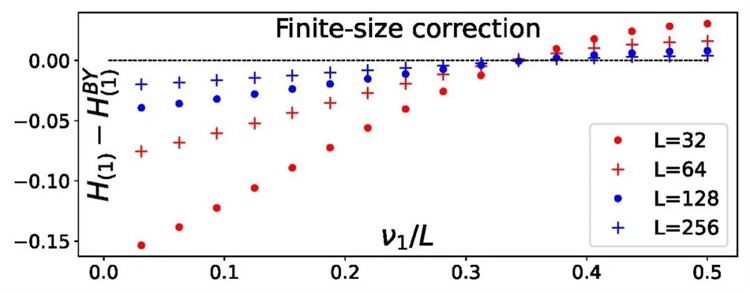
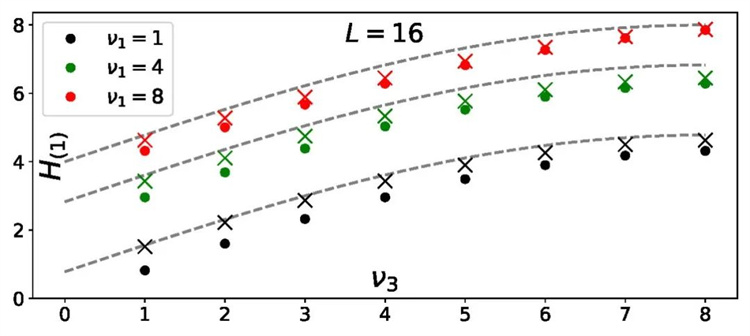
這項研究有望進一步闡明弦理論、量子場論和量子可積系統之間錯綜復雜的關系。該團隊的工作仍處于早期階段,但它標志著我們對理解AdS3/CFT2對偶及其在理論物理中的影響向前邁出了重要的一步。